
Blockchain technology has been one of the most exciting and revolutionary discoveries of the new century. While residing on mathematical and economical ideas which have existed for a long time before it was invented, blockchain has just recently found wide application in cryptocurrency related projects like Ethereum or Bitcoin. One such idea, which has been a key building block of the blockchain technology, is the idea of hashing.
Hashing is a mathematical process that takes various input data and performs a complicated operation on it, after which it releases the result of the operation as a fixed-size output data. The size of input data (which is also called a string or a message) doesn’t matter, however the returned output (also called a digest) will always be of a fixed length.
In the context of Bitcoin, the input data are its transactions. These transactions are put through a hashing algorithm (BTC uses a SHA-256 hashing algorithm) which results in creation of a fixed length output.
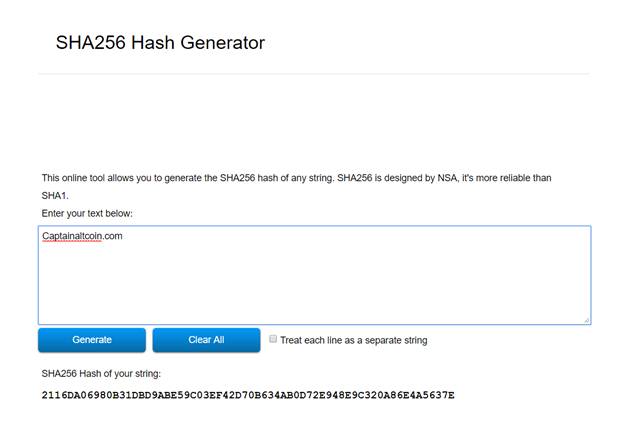
SHA-256 algorithm will take any input and convert it into a 256 bits long hash output
Hashing algorithms will always create an output that is fixed in size, whether you used a single letter or Tolstoy’s War and Peace as your input. With blockchain, the input is the complete blockchain (namely its transactions); the output is the current state of the blockchain put through the SHA-256 algorithm. The importance of hashing is immense for the blockchain, as it allows data of literally any size to be stored simply and effectively. It also allows the parties involved (miners, transactors, the network) to agree on the current state of the chain. Alongside digital signatures, hashing is one of the two main cryptographic concepts which underpin the blockchain technology.
Let’s look at the Bitcoin blockchain directly for a moment. Its blockchain is, as the name implies, made out of blocks, which are basically data storages filled with transactions. If we go back, we will notice that the blockchain has a so-called genesis block. This is the first, original block of the blockchain which contains the first ever made transactions with Bitcoin. These transactions were “packed” inside the genesis block and were used as inputs to the SHA-256 hash algorithm, the choice hash algorithm of the Bitcoin blockchain. For every new block, the previous block’s hash output is used as one of the inputs for generating said new blocks hash output, alongside its transactions. The now generated second output will be used as an input for the output of the following block etc. This is how we form a chain of blocks, or a blockchain, where each hash creates a link between two successive blocks.
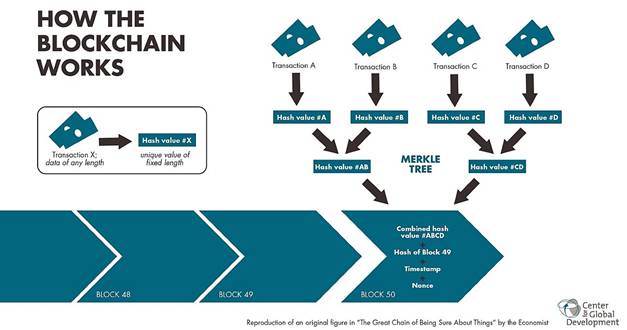
Source: https://www.investopedia.com/news/top-blockchain-startups-watch-2018/
This system guarantees that no past transaction can be tampered with, because if any transaction is changed, that means that the inputs to the blocks hash function are changed. Once you change these inputs even the slightest, a new hash output will be generated that looks nothing like the original. And a new hash output clearly means that the inputs to the following blocks hash function will be different and will have a completely new output. This-tamper proof system ensures that everyone simply needs to agree with the 256 bits of data provided by the hash algorithm. Otherwise, the network would need to re-verify all the previous gigabytes of transaction data each and every time a new block is added.
Hash functions have been used in mathematical and computational processes (like hash tables) before and have recently found application in cryptography. However, the adjective “cryptographic” gives the hash functions a specific dimension, as it implies that they need to possess a certain set of design qualities and properties which make them suitable for use in cryptography and security. Cryptographic hash functions have many security and privacy-related applications, notably in digital signatures, message authentication codes (MACs), e-commerce protocols and other forms of authentication.
What you'll learn 👉
Cryptographic hash functions properties
- Efficiency
A cryptographic hash function needs to be computationally efficient, in the sense that it shouldn’t take a lot of time to convert an input into an output. While a more complicated hash function is definitely safer, taking too long to process the input into a hash output will make the function inefficient.
- Determinism
No matter how many times you parse a particular input through a hash function you will always get the same result. This is critical because if you get different hashes every single time it will be impossible to keep track of the input.
- Collision resistance
It should be difficult to find two different inputs A and B which have identical hash outputs. This is extremely important in the context of digital safety. While it is mathematically possible that two inputs will eventually have the same hash output, it should be astronomically difficult to find these two inputs. Such a pair is called a cryptographic hash collision and being resistant to it is sometimes referred to as strong collision resistance. Lacking this resistance means that the algorithm is vulnerable to collision attacks. Collision resistance is a concept which often comes with two other resistances:
Ø Pre-image resistance
It should be difficult for a malicious player to find any input based on what its hash output looks like. The function needs to be one-way only. This feature of cryptographic hash functions is closely related to their deterministic nature, which means that any given input will have a single, set hash output. Functions that lack this resistance are vulnerable to preimage attacks. The only method that one has to find the original input is by using the “brute-force method”. Brute-force method basically means that you have to pick up a random input, hash it and then compare the output with the target hash and repeat until you find a match. This approach can result in three scenarios: 1) Best case scenario, where you get a match on the first try itself. The odds of this happening are astronomical 2) Worst case scenario, where you get your answer after 2^ bits that the hash has – 1 times. Basically, it means that you will find your answer after trying out every possible input 3) Average scenario, where you will find it somewhere in the middle. This will also require an astronomical amount of guesses.
Ø Second pre-image resistance
From a given input A, it should be difficult to find an input B which has the same hash output as the input A. Functions that lack this resistance are vulnerable to second-preimage attacks.
Collision resistance has long been an important issue in the cryptography community. Many times we saw people create seemingly collision resistant functions, just to have someone swoop in a year later with a way of causing collision in the algorithm. An important and interesting problem is related to the issue of collision resistance; its name is the birthday problem or the birthday paradox.
Let’s say you find yourself in a room with a random stranger. You might ask yourself: I wonder if the two people in this room are born on the same day of the year. Chances are the two of you don’t have the same birthday. In fact, the probability that the two of you were born on the same date is 0.0027, or 0.27%. From here on you might deduce two things. First of all, you might think the probability that at least two people in your room were born on the same day will jump to 100% once there is a total of 366 people in there. This would be true. Second, if a new stranger joins the two of you in the room, you might assume that the chances of two of the people in there having the same birthday will double from when there were only two people. This would be false, and this is the issue of the birthday paradox.
It would be mathematically difficult to calculate the probability of there being a shared birthday within a set of people – so we instead calculate the opposite – the probability of no one sharing a birthday. The formula used for this will look like this:
![]()
where P stands for probability.
Probability of someone in an n number of people not being born at the same day as you can be calculated by using another specific formula:
![]()
Then this number is subtracted from 1 which will give us the probability of someone from that n number of people being born on the same day.
Let’s take the previously mentioned example of three people. The P (no match) for this group will be:
![]()
The P (match) for this group will then be:
Meaning that there is 0.82% probability that two people in that room have the same birthday.
The birthday problem is fascinating because it is the result of comparing individual probabilities against each other. As each person is added to the room the chance of two people in there having the same birthday increases, as each new person is compared to each person that was previously there. This results in a an exponential, rather than linear, growth of the probability and creates a trend that looks something like this:
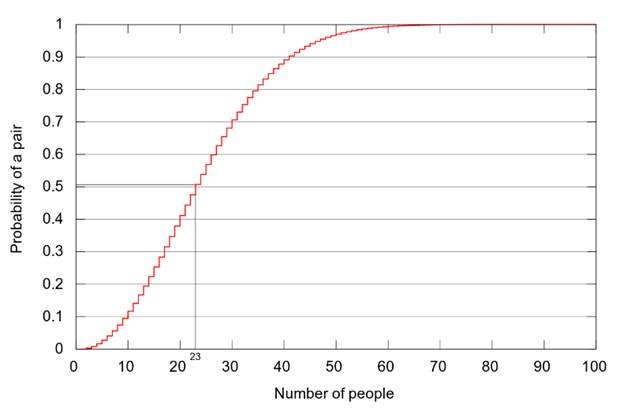
Clearly the growth is exponential, with the probability raising to 50% at just 23 people and reaching 99% somewhere around 70.
This paradox has found application in the so called birthday attack, a cryptographic attack whose goal is to use brute force to find two different inputs which will give the same output when put through a hash function. Basically, its cause is to create a collision. Because of the birthday paradox, the brute force method of creating collision is much more efficient than it should be. However, the probability that the collision will happen still remains astronomical. To apply this to the Bitcoin network, an attacker, after doing the physically impossible a 3 trillion times over, has only a one in a trillion chance of getting even one satoshi out of the successful collision. Bitcoin’s current algorithm, SHA 256 still hasn’t had its collision resistance broken but there are already plans to switch to a completely new SHA-3 generation of algorithms in the future. This problem is explained in more mathematical detail here and here.
- Privacy
A hash function needs to be able to hide information about the input. Looking at the output, it should be difficult to determine the properties of the original message that was put through the hash function. If a malicious player is able to gather even the slightest bit of information, say if the input was an even number or an odd one, the hash function isn’t secure enough.
- Randomness
The final output of the hash function needs to be properly distributed, random. The full definition says: For every output “Y”, if k is chosen from a distribution with high min-entropy it is infeasible to find an input x such that H(k|x) = Y.
High min-entropy means that the distribution from which the value is chosen is hugely distributed so much so that us choosing a random value has negligible probability. Basically, if you were told to choose a number between 1 and 5, that’s a low min-entropy distribution. However, if you were to choose a number between 1 and a 2^256, that is a high min-entropy distribution. The “|” denotes concatenation. Concatenation means adding two strings together. Eg. If I were to concatenate “CAPTAIN” and “ALTCOIN” together, then the result would be “CAPTAINALTCOIN”.
Suppose you have an output value “Y”. If you guess a random value “k” from a wide distribution, it should be infeasible to find a value X such that running the concatenation of k and x through a hash algorithm will give the output Y. This is a concept that is implemented in the process of Bitcoin mining.
The final output should look as if a set of coin flips took place in creating it. Of course this won’t be the case as the underlying hash algorithm will always make the same, fixed output for each input. A good hash algorithm will have the output distributed well enough to make a malicious player unable to deduce any patterns which could lead to revealing information about the original input.
An in-depth look at hashing data structures
A data structure is basically a way of storing data. To understand how a blockchain works we need to take a look at two important elements of a data structure: pointers and linked lists.
- Pointers
Pointers are variables in programming which store the address of another variable. Normally, variables in any programming language store data. For example int a = 10, means that there is a normal variable “a” which stores integer values (with the actual value being 10). Instead of storing numeric values, pointers store addresses of other variables. Since they are literally pointing towards the location of other variables, they were named pointers.
- Linked Lists
Linked lists are important parts of data structures. A linked list looks like this:
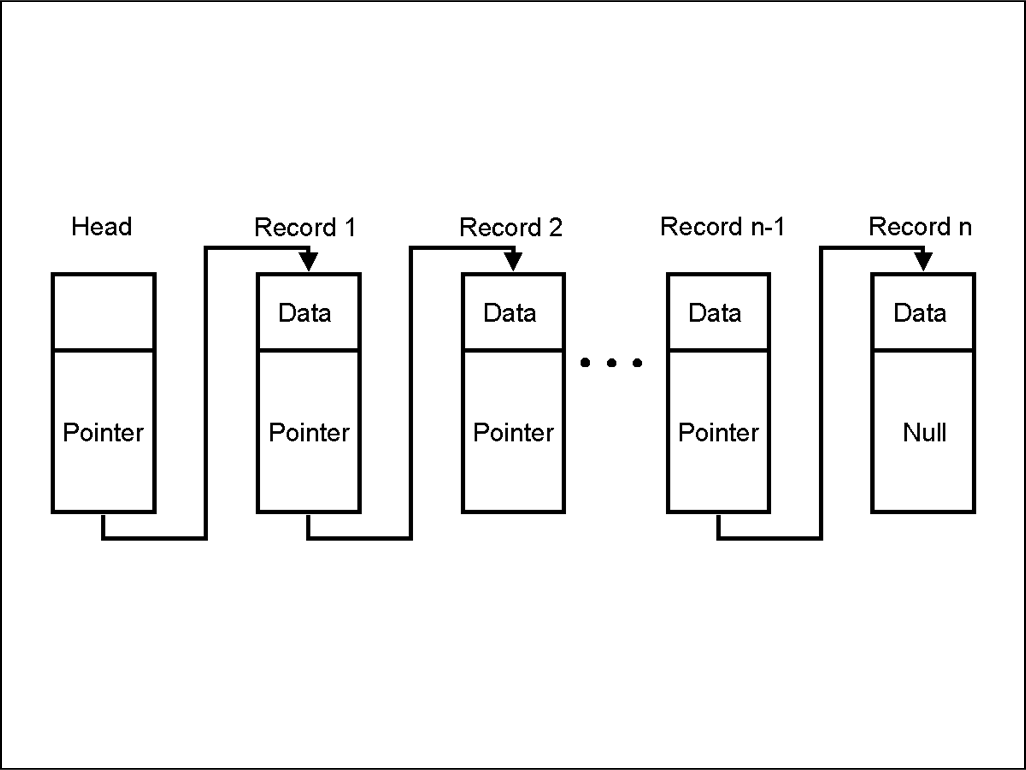
As you can see this is a chain of blocks (rings any bells?), where each block contains data and is linked to the next block by a pointer. The pointer contains the address of the next data block. The last block has a so called null pointer, meaning that it currently has no value. The value can be added later, once the next block is created. As you may have guessed by now, this is what the structure of the blockchain is based on. A block chain is basically a linked list and its structure looks like this:
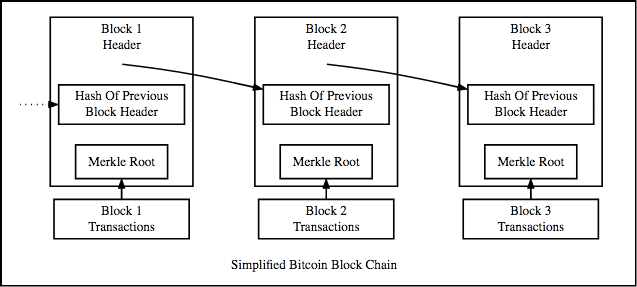
Clearly a blockchain is a list of linked blocks which contain data and a special kind of pointer, called the hash pointer, which points to a previous block and creates a chain. With a hash pointer, the address of the previous block is basically its data that has been hashed, or put through a hash algorithm. Hashing the blocks data gives us a unique pointer which will be safe to use as a link between two blocks.
While it’s clear that each block contains the pointer of the previous block, one might notice a problem and ask the question: where does the pointer of the genesis block stay?
The genesis block doesn’t have a pointer going into it. It does however have a pointer that links it to the block no.2, and this pointer is created by hashing the data which is stored in the genesis block.
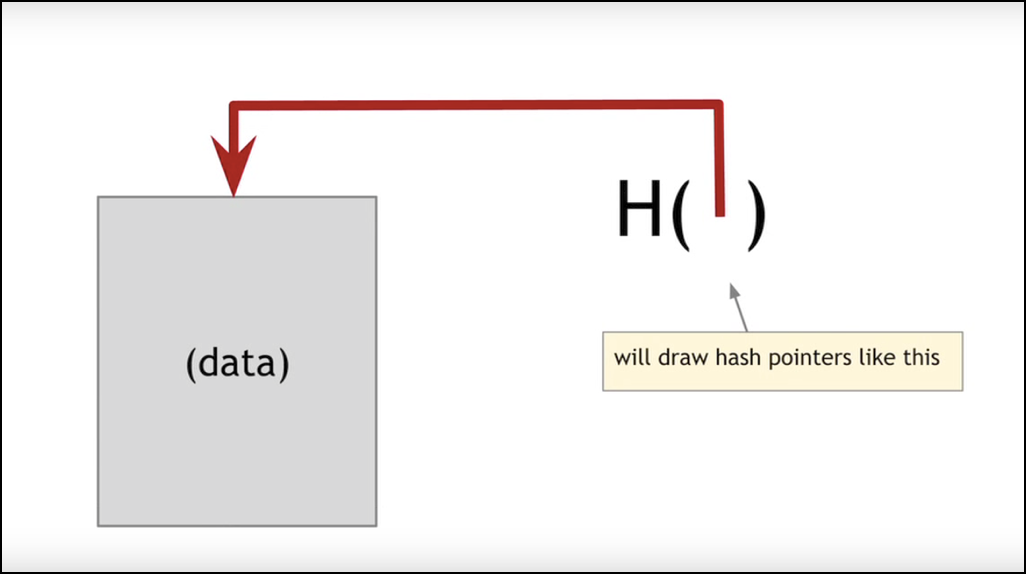
Image source: https://www.coursera.org/learn/cryptocurrency/lecture/EYEAo/hash-pointers-and-data-structures
If an attacker was to attempt a hack on this chain in order to change its data, this system would automatically repel the attack. Because of the way hash functions are generated, a slight change in input data will completely change the resulting output. Say you made changes on the block 23; this will change the hash pointer which is stored in block 24, which will also change the data of the block 24 and the hash output which will be used to connect to the block 25, etc. This will completely change the chain, making everyone involved aware that this isn’t the original chain. This is exactly how blockchains attain immutability.
Each block inside the Bitcoin blockchain needs to be identified somehow. Otherwise, it would be impossible to track them. This identification is done via the block header, and currently each block contains the following:
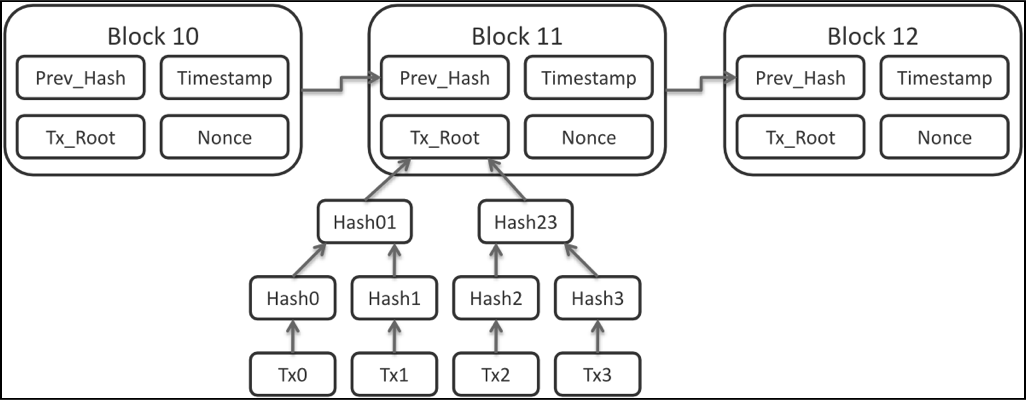
A block header contains:
- Chain version number (used to keep track of upgrades and changes in protocol)
- Current timestamp of the block in UNIX (number of seconds since January 1, 1970)
- The difficulty target of the block (number of zeroes that must be found when hashing the block header in order to meet the level of proof of work required to maintain the block creation time around 10 minutes)
- Hash of the previous block (hash pointer)
- Nonce (the value used by miners to generate a correct hash)
- Merkle root hash of the said block’s transactions
All of these parts play an important role in the creation of a block; however the nonce and the Merkle tree deserve special attention. The nonce is the value that is altered by the miners in the process of cryptocurrency mining to try different permutations. Trying different permutations is how we achieve the difficulty level required – the more permutations, the more difficult the mining process is.
In the diagram above you can see a typical Merkle tree. On the bottom are so called leaf nodes. These leaf nodes are built upon by non-leaf nodes. Each non-leaf node is basically a hash of a previous, child node. Finally, at the top of the tree is the root node.
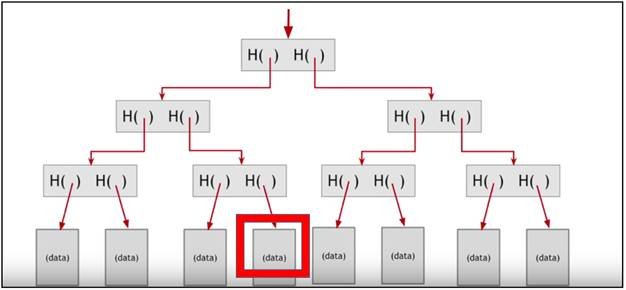
The Merkle tree is applied in cryptocurrencies as a solution for the storage space and time which would be required if we were to store each and every transaction on the blockchain.
If we want to find out if a piece of data belongs in a certain block, we can simply trace its hashes down the Merkle tree all the way to the block we want to check.
How does this all relate to Bitcoin?
Bitcoin mining is basically searching for a new block to be added in the blockchain. Every blockchain is based on the Merkle architecture, with blocks basically being the leaf, non-leaf and child nodes. Miners from around the world are constantly “working” to make sure that the chain keeps on growing. The mining process itself is a proof-of-work-based system where a miner is offering his computational power to the Bitcoin network which is then used for hashing data (creating hash outputs from the input data through the SHA-256 algorithm). This hashing power is added to the total hash rate of the Bitcoin blockchain. Hash rate basically means how fast the network of miners is able to conduct the hashing operations. A high hash rate means more miners are taking part in the mining process and as a result the difficulty level (or the amount of work that needs to be put in by the miners) is increased. If the hash rate becomes too low then the difficulty level is decreased as well.
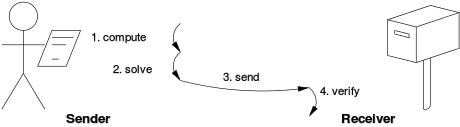
As seen on the image, the miner uses computational work to solve a so called challenge string, which is a string of numbers that begins with multiple zeros. The more zeros it starts with, the harder the mining process is. The miner “solves” this string by finding a response string (proof string). The only way to find this solution is to invest a lot of computational power to first hash the transactions from the mempool and create a new block, then add a random value through the nonce and create a possible solution. This concatenated response string is taken by the network and ran through a hash function to determine if the output will be equal or less of the challenge string. . If it is not less than the difficulty level, then the nonce will be changed millions of times until finally, the requirements are met. When that happens the block is added to the blockchain.
If we remember the previous requirement of randomness we mentioned a formula: for every output “Y”, if k is chosen from a distribution with high min-entropy it is infeasible to find an input x such that H(k|x) = Y. If we apply this to Bitcoin mining, the variables will be as following:
- K = Nonce
- x= the hash of the block
- Y = the difficulty target
The entire process of nonce selection is completely random and brute force based. The mining software will keep on randomly generating strings until a solution is found.
The more zeros the output contains, the more work was put in to get the solution. For an output which contains 40 zeros, a computer will on average need to try about 2 to the power of 40 solutions before finding the correct one (more or less is possible, depending on luck). The blockchain then runs a hash function to check if the proof is valid (if it contains enough zeros – currently the requirement for Bitcoin network is extremely high) and if that is the case the block is added to the blockchain. The difficulty is currently set at 10 minutes per block added, as the network feels this is an acceptable speed of releasing new Bitcoins which ensures low collision probability and lowers the number of orphan blocks (blocks that aren’t added to the blockchain because their miner didn’t find the solution). The difficulty is readjusted every 2016 blocks.
Hashing is clearly an important part of the Bitcoin network as it enables the underlying proof-of-work algorithm to function properly. It is an efficient, private and fast system which offers unmatched collision resistance and security. Without hashing and its revolutionary concepts, the blockchain as we know it today wouldn’t exist.







