
Anyone who spent more than a couple of minutes conversing about Bitcoin and cryptocurrencies in general has probably been introduced to the term “cryptographic hash function”. In the same breath, that person’s conversation partner might have mentioned some even stranger sounding words like DSA, MD5, SHA-1, SHA 256, RIPEMD, BLAKE and various other “cryptographic hash algorithms”. Cryptographic hash functions are important elements of modern information security; they are also the underlying algorithms which serve as the building blocks of the current Bitcoin blockchain and allow it to be decentralized and secure.
Generally a hash function is a mathematical process that takes various input data and performs a complicated operation on it, after which it releases the result of the operation as a fixed-size output data. The size of input data (which is also called a string or a message) doesn’t matter, however the returned sequence (hash function also called a digest) will always be of a fixed length.
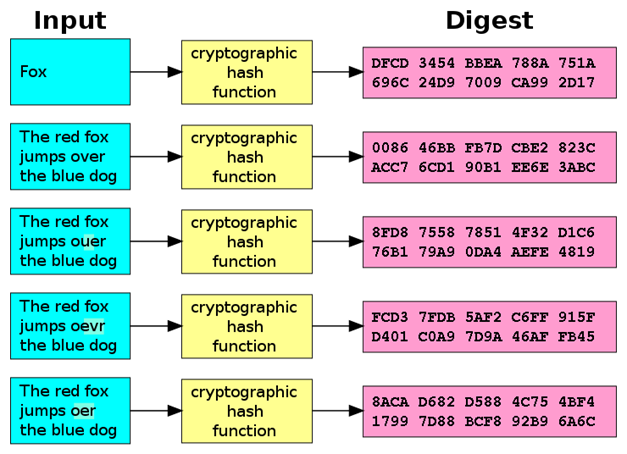
Image source: https://en.wikipedia.org/wiki/Cryptographic_hash_function
A common use for this kind of hash function is to store passwords. Almost every website you visit nowadays requires you to create a user account, which needs to be protected with a password. When you create your user account on such a website, the password you chose will be used as input in a hash function; the function will run and the hash output is stored on the website servers. Every time you attempt to log into your account you will be asked to type your password in a provided area; the same hash function from before will be run on the word you enter, and if the resulting output matches the stored output, you will be granted access to your account.
Hash functions have been used in mathematical and computational processes (like hash tables) for quite some time now and their use in cryptography has just recently become a thing. However, the adjective “cryptographic” gives these hash functions a special dimension, as it implies that they need to possess a certain set of design qualities and properties which make them suitable for use in cryptography and security. Cryptographic hash functions have many security and privacy-related applications, notably in digital signatures, message authentication codes (MACs), e-commerce protocols and other forms of authentication.
What you'll learn 👉
Cryptographic hash function properties
Key properties that one cryptography-viable hash function needs to have are:
- Efficiency
A cryptographic hash function needs to be computationally efficient, in the sense that it shouldn’t take a lot of time to convert an input into an output. While a more complicated hash function is definitely safer, taking too long to process the input into a hash output will make the function inefficient.
- Collision resistance
It should be difficult to find two different inputs A and B which have identical hash outputs. This is extremely important in the context of digital safety. While it is mathematically possible that two inputs will eventually have the same hash output, it should be astronomically difficult to find these two inputs. Such a pair is called a cryptographic hash collision and being resistant to it is sometimes referred to as strong collision resistance. Lacking this resistance means that the algorithm is vulnerable to collision attacks. Collision resistance is a concept which often comes with two other resistances:
Ø Pre-image resistance – It should be difficult for a malicious player to find any input based on what its hash output looks like. The function needs to be one-way only. This feature of cryptographic hash functions is closely related to their deterministic nature, which means that any given input will have a single, set hash output. Functions that lack this resistance are vulnerable to preimage attacks.
Ø Second pre-image resistance – From a given input A, it should be difficult to find an input B which has the same hash output as the input A. Functions that lack this resistance are vulnerable to second-preimage attacks.
Collision resistance has long been an important issue in the cryptography community. Many times we saw people create seemingly collision resistant functions, just to have someone swoop in a year later with a way of causing collision in the algorithm.
- Privacy
A hash function needs to be able to hide information about the input. Looking at the output, it should be difficult to determine the properties of the original message that was put through the hash function. If a malicious player is able to gather even the slightest bit of information, say if the input was an even number or an odd one, the hash function isn’t secure enough.
- Randomness
The final output of the hash function needs to be properly distributed, random. It should look as if a set of coin flips took place in creating it. A good hash algorithm will have the output distributed well enough to make a malicious player unable to deduce any patterns which could lead to revealing information about the original input.
A good cryptographic hash function can be compared to a meat grinder; it takes a bunch of original pieces, puts them through the grind of a mathematical algorithm and creates something that looks nothing like what was originally inserted into it while being practically impossible to recreate the original pieces from the output. These functions can be used in various ways, namely for verifying file integrity, creating proof of work, generating/verifying passwords and keys etc. Recently, they found new application and became key elements of Bitcoins proof of work system of coin mining.
Proof of Work
A proof-of-work system is a computational, economic measure designed to deter denial-of-service attacks and other service abuses such as spam on a network by requiring some work from the service requester, usually meaning processing time by a computer. A proof of work system is similar to a puzzle, where a requester takes on a task of connecting the pieces and creating the correct solution to a problem that was set up by the other side, in order to receive a service from the provider. A key feature of a proof of work system is its asymmetry: the work must be moderately hard (but feasible) on the requester side but easy to confirm for the service provider.
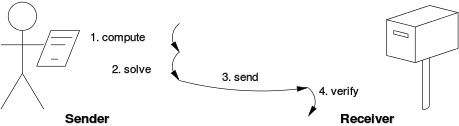
As seen on the image, the miner uses computational work to solve a so called challenge string, which is a string of numbers that begins with multiple zeros. The more zeros it starts with, the harder the mining process is. The miner “solves” this string by finding a response string (proof string). The only way to find this solution is to invest a lot of computational power to first hash the transactions from the mempool and create a new block, then add a random value through a nonce and create a possible solution. This concatenated response string is taken by the network and ran through a hash function to determine if the output will be equal or less of the challenge string. If it is not less than the difficulty level, then the nonce will be changed millions of times until finally, the requirements are met. When that happens the block is added to the blockchain.
The hash function needs to be applied only once to confirm whether the solution is good or not and whether the requester performed the required amount of work to find it. If the solution is good, the provider grants the requester the right to use a service. This system enables the previously mentioned asymmetrical architecture and is at the core of every proof-of-work-based algorithm.
Bitcoin mining and Bitcoin Hash
How does this all apply to Bitcoin and Bitcoin mining? Well, Bitcoin mining can be observed as an action performed by a miner (requester), who offers his computational power (CPU or GPU) to help the Bitcoin network (provider) with transaction verifying, in exchange for Bitcoin. A miner searches the Bitcoin mempool (storage for unconfirmed transactions), finds the ones which he wants to verify, adds them to a new block and then attempts to find the proof string which will be sent to the Bitcoin networks blockchain. The blockchain then runs a hash function to check if the proof is correct (if it contains enough zeros – currently the requirement for Bitcoin network is extremely high) and if that is the case the block is added to the blockchain.
Currently it takes about 10 minutes for the miners to discover the new block. The mining difficulty itself aka the number of zeros required is adjustable and changes every 2016 blocks. This change of difficulty is done to preserve the average block creation time. The mining process comes with two awards: First of all the miner gets a cut of the transaction fees that are attached to each transaction he verifies. He will get the second award if his proof of solution is accepted by the network and it comes in the form of newly minted Bitcoins that are created every time a new block is added to the blockchain.
We can compare this system to a locked safe which contains a reward; each time you want to access this reward you need to solve the safe combination. Except the code is hashed, where a part of the combination is written on the safe, and the rest is upon you to figure out yourself. Imputing it correctly will give you access, while a failed attempt resets the lock and forces you to try again. Obviously the process is much more complicated and mathematical in actuality but the abovementioned should give you a quick rundown on how it works.
Hashing is clearly an important part of the Bitcoin mining system and it enables its underlying proof-of-work algorithm to function properly. It is an efficient and collision resistant solution which offers unmatched speed, privacy and security. Whereas BTC currently uses a SHA 256 hashing algorithm, which is a part of the SHA-2 generation of algorithms and still hasn’t been compromised by collision attacks, there are plans to implement a new generation of SHA-3 algorithms in the future. It remains to be seen how Bitcoin will react and if it will switch onto this new infrastructure.







